О модели войны я уже писал. Модель распределения сложнее. В экономике за модели поведения человека Нобеля дают. Но проще — понятнее. Пересказываю Хабра.
Эта модель посложнее модели войны. Человечеству надо как-то распределять произведённые блага. Их число ограничено Eo ., так же как и число людей No . Распределение благ по людям считаем непрерывным ( No ≫1). Считаем нарастающим итогом распределение благ. Начинаем с бедных и идём к богатым.
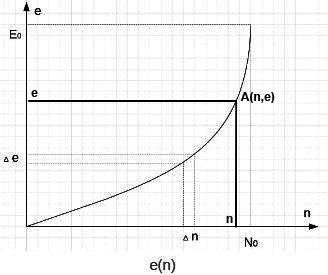
В (·) А n человек получили на всех е благ. Производная ф-ции e(n) – блага полученные одним человеком в группе Δn (Δe/Δn ) . Отнормируем и сделаем безразмерными координаты. e ➞ e/Eo ; n ➞ n/No .Заодно поменяем местами оси, будем работать с обратной ф-цией. Получим:
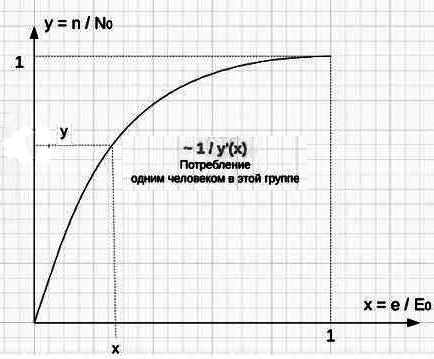
А теперь попробуем найти условие минимального страдания человечества. Для этого грубо предположим, что страданий тем меньше, чем больше благ получает человек, т. е. ф-ция страдания ξ(x)=Ay'(x) . Тогда страдание человечества просто интеграл от этой ф-ции:
S=∫ξ(x)dy = ∫ξ(x)y’dx =A ∫y’² dx .
Но подбор ф-ции, которая минимизирует интеграл (страдание), хорошо известно в механике. Это лагранжиан свободно двигающейся по прямой материальной точки. Решение отлично известно, кинетическая энергия сохраняется, а у нас с учётом условий y(0)=0 и y(1)=1, y(x)=x, а доход на любого человека Eo/No — поровну.
Можно попробовать чуть усложнить и написать ξ(x)=Ay'(x)-B/y'(x) , т. е. учесть, что человек получает кроме страданий и удовольствие и это удовольствие тем больше, чем больше в его распоряжении благ.
Ответ тот же – y(x)=x ; блага ~ кол-ву людей; всё поровну!
А теперь займёмся завистью. Пусть в нашей модели человек страдает, узнав, что кто-то живёт лучше, и получает удовлетворение когда кому-то хуже. Тогда ξ(x)=Ay'(x) – Bf(y(x))/y’(x) .
Зависть штука сложная, поэтому разложим её в ряд Тэйлора удержав линейный член:
ξ(x)=Ay'(x)-B(1+Cy(x) )/y'(x) . C здесь коэф. зависти.
Теперь надо подбирать подходящую ф-цию вида Ay’² – B – Всy , а это уже лагранжиан точки в поле ~x (mgh). Если обозначим α = С/4А , то подходящая ф-ция уже y = (1+α )x- αx ².
Зависть убила равномерное (справедливое?) распределение! Причём чем больше зависть (С) тем богаче становятся богатые, а бедные беднеют. (подробности в ссылке).
PS Биологически зависть можно оправдать. Если уровень бедности на уровне физиологического выживания (а то и ниже), то зависть может быть полезной для выживания. Такой уровень бедности преодолён не так давно в развитых странах (см. например Оруэлл «Фунты лиха в Париже и Лондоне», 1933 г.).
Единственно чем в нашей модели мы можем скомпенсировать зависть, это ввести в функцию страдание, если ты живёшь лучше других. Единственно мирным путём. Но можно ещё насильно поделить. И то, и другое – выбор общества. Как и выбор — надо ли всё делить точно поровну.

Очень интересно,Андрей, спасибо.Сейчас видно ученого-все Вы пытаетесь свести к формулам, и богатство, и бедность, и зависть.К сожалению, на формулах тут не проедешь-зависть иррациональна.Есть хорошая притча про зависть:”Бог сказал человеку-дам тебе все, что хочешь-но с условием, что соседу твоему дам в два раза больше.Теперь говори-что желаешь?”Человек ответил:”Всемогущий, вынь у меня один глаз!”Вот как-то так..
Анне. Все модели очень слабенькие. Меня забавляет, что из самых простых предположений можно сделать интересные выводы. Модели общества показывают только то, что мы и так знаем. Но не только наглядны, но в силу уважения к математике убедительны