…не на выставку поделок из некрашенных корней
Иваси
Помните, была такая мода. У меня кое-что сохранилось несмотря на переезды.
Живут, где могут, по всей квартире
горе, горе крокодил …
Чуковский
А сегодня иду на работу, батюшки, зимний крокодил!
Такие у меня природные зоопарки
Доброе утро!Хочу рассказать об интересном эпизоде, который приключился со мной вчера.Гуляю это я, как обычно, в нашем парке Сосновка-и вдруг ко мне обращается молоденькая девушка с детской коляской.Я думала, она дорогу хочет узнать-а она спрашивает, как надо дарить новогодние подарки..
Удивилась я такому вопросу от незнакомого человека-но стала объяснять на полном серьезе, что это зависит от того, кому дарят, от отношений с людьми и пр.Говорю ей:”Вы уж, наверно, приготовили подарки для мужа?”А она отвечает, что не замужем и ребенок не ее-она только нянька.Удивилась я еще больше-но продолжаю давать рекомендации(мол, можно дарить деньги, косметику, спиртное, продукты, открытки и клипы и пр.)А девушка говорит, что, мол, дарить подарки на Новый год слишком банально-лучше дарить их неожиданно и без повода.Призадумалась я, вспомнила свой опыт работы гувернанткой-и говорю:”Конечно, так тоже можно-но советую не забыть поздравить ваших работодателей с Новым годом, хорошее их отношение вам не помешает”.Кажется, такой взгляд для девушки был внове-поблагодарила меня и мы расстались..
А далее я не выдержала и все же купила ветки сосны-хотя искусственную елку уже нарядила.Публикую фотку наряженной ветки-только прошу прощения, что неважно вышло.Писала уже, что в моем новом мобильнике плохая камера.Кстати, за елкой висит не картина-а моя собственная вышивка.Обязательно сделаю как-нибудь пост с моими вышивками-после Нового года..
Вот такие были дела-с наступающим Вас!
Лет двадцать назад в нашем дачном посёлке (тогда ещё совсем небольшом) на столбе у магазинчика появилось объявление на обрывке старых обоев.
Объявление, прямо скажем, на объявление совсем не похоже. Крик души: “Гады!!! Верните бочку на место! Раз я одинокая женщина, надо мной можно издеваться?”
Поначалу я решила, что речь идёт о садовом инвентаре – бочке для поливной воды… Но соседи просветили. Речь шла о пивной бочке, не очень больших размеров, которую утром привозил, а вечером уже пустой увозил небольшой пикап. Продавщица была местной, хорошо знакомой всем проживающим в посёлке. А так как она частенько разбавляла пиво водой, народ решил её проучить. как только она удалилась по своим нуждам, подъехал трактор и укатил бочку на местный пляж. Вскоре все мужики посёлка, плюс отдыхающие умчались туда же. Знатно повеселились. На халяву и разбавленное пиво сошло :))
Пустую бочку к вечеру вернули на место. Правда, за пиво не расплатились. Пришлось ей свои деньги выложить. Но больше она пиво не разбавляла.
Так что народный способ борьбы за качество оказался весьма эффективным.
Решила отпылесосить в книжных шкафах и разобрать папки со своими записями, чтобы ненужное выбросить. Наталкиваюсь на такие, о которых давно забыла. Посмеялась и решила вас посмешить.
К уроку понадобилась репродукция Джоконды. Большого размера, чтобы с последней парты было видно.В магазине приглянулась подходящая. Выбила чек. Говорю продавщице:”Девушка, подайте мне, пожалуйста “Джоконду”
-Чего?
-Репродукцию. Монну Лизу
Не понимает. Вынуждена показать пальцем. И тогда она говорит своей напарнице:
-Даша, принеси женщине Лизавету
***
Афиша перед ДК “Котельщик”, на которой ВИА Гра. Расшифровываю:Вокально-инструментальный ансамбль Гра (Гра-Игра с украинского)
Дамочка, увидев афишу: “Сколько можно! Скоро из утюгов эта реклама полезет. Да лучше бы продавали нашим мужикам такие таблетки, чтоб ума побольше было! И не мыкалась бы Россия, народ бы не страдал… А то об одном только месте заботятся, чтобы хорошо работало. А где надо ум приложить – там не работает.
Приболел как-то у меня внук, и я пошла с ним в поликлинику.
Почти на каждой двери в кабинеты врачей прикреплены объявления: “Дилерам и распространителям не входить!”
Внук говорит: “Бабуля, а мне туда тоже нельзя входить”.
Удивилась, но решила уточнить:”Это почему?”
На полном серьёзе, даже сказала бы – озабоченно:”Как почему, я ведь тоже распространитель…”
-И что же ты распространяешь?
-Как что? Инфекцию…
P.S. фото из интернета, то есть, это чужой внук :))
ячейка Бенара
В Ньютоновской механике время было простым параметром. В системах из одного-двух тел можно было поменять знак у времени и скоростей, — и концы в воду. Никто ничего не заметит. Если уж система прикатила из “А” в “В”, то она столь же хорошо, по той же траектории укатит из “В” в “А”.
Потом появились паровые машины, стали интересоваться многочастичными (больше двух) системами и возникла термодинамика.
В задачах термодинамики частиц было много, а интересовалась она вначале равновесными состояниями. Выяснилось, что равновесные состояния просто наиболее вероятные (второе начало, возрастание энтропии). Время уже не повернёшь, смесь так просто не разделяется по бутылкам из которых выливали компоненты, но упорядоченной структуры тоже не получишь. Можно даже посмотреть, как поведет себя система, если слегка нарушить равновесие (капнуть из одной бутылки). Предсказуемо поведёт. Более того, её поведение зависит от граничных, а не начальных условий. Существенно, что эволюция системы руководствуется величиной какого-нибудь потенциала, не энергией, так свободной энергией (F=U-TS). Конечное её состояние определяется однозначно и эволюцию живого не напоминает, память о прошлом не сохраняет.
Но как только отклонение от равновесия становятся достаточно велики, переходят “красную черту”, возникают варианты. Система становится способной усложниться и приобрести макроскопическую пространственную или временную структуру. Более того, эта структура зависит от начальных условий, причём так, что незначительные вначале различия нарастают как снежный ком (погода) и становятся принципиально непредсказуемы. Вдали от равновесия система может стать крайне чувствительна к внешним полям. Несущественный в равновесии толчок может загнать её в новое состояние.
Итого, впадая в грех редукционизма, можно прийти к выводу, что не только под лежачий камень вода не течёт, но и любая система в слабонеравновесном состоянии склонна к деградации, но никак не к усложнению.
Насколько это хорошо – дело вкуса.
“Игрушечников” много в нашей жизни. Просто надо уметь видеть их и радоваться тем играм, что они нам предлагают.
Просматривая публикации газеты «Don Day» натолкнулась на заметку: «Туристический поезд на паровой тяге будет курсировать в новогодние праздники из Ростова в Таганрог. Об этом 18 декабря сообщил портал «Электрички Кавказа».
Этот поезд и раньше курсировал в памятные даты Таганрога: в День освобождения города, в День Победы и в День города. Один вагон полностью – музей. Каждый раз в нём новая экспозиция.
Новый год «игрушечники» предложили тоже встретить необычно: в составе, который будет тащить за собой настоящий паровоз.
Помимо самой поездки «на поезде паровой тяги» (что само по себе – уже приключение), жителям и гостям Дона предлагают купить готовый тур «Зимняя сказка» с новогодней развлекательной программой и автобусной экскурсией по моему замечательному Таганрогу.
Приезжайте в гости!
Я обратил внимание, что зачастую идея жизни в 4х мерном мире вызывает зябкое раздражение. Тем более, что повлиять на 4ое измерение сложновато, оно какое-то очень независимое от нас.
Но есть объекты, которые сами по себе — мир иррациональных измерений. Например облако.
Но сначала, а как определить мерность объекта?
Как мы измеряем? Берём и сравниваем с эталоном. Так, чтобы измерить дециметровый отрезок, надо взять 10=101 сантиметровых платиновых «спичек»; для измерения квадрата со стороной дециметр надо взять 100=102 платиновых квадратика; для кубика надо запастись 1000=103 сантиметровых кубика. Т.е. размерность объекта содержится в показателе степени.
А теперь посмотрим на объект похитрее — множество Кантора (канторова пыль,).
Строится просто (простейший фрактал). Делим единичный отрезок на 3 части и выбрасываем середину. Повторяем заклинание на каждом из оставшихся отрезков. И так до бесконечности .
Измеряем. Для измерения двух отрезков длиной 1/3 нужно два эталона длиной 1/3.
Далее потребуется 4 эталона по 1/9 ; потом 8 эталонов по 1/27. На n–ом шаге потребуется 2n эталона длиной 1/3n . Тогда размерность «пыли» естественно определить из соотношения 2n=(3n)d , откуда размерность d=log32 , вполне иррациональное число. Такая размерность выгляде чудесатее, нежели скромная цифра четыре.
Непривычно. Хотя ничего необычного здесь нет. Фракталы окружают нас. Папортник (не обязательно Барнсли)
Или такое высказывание (https://scask.ru/d_book_fract.php?id=60): при исследовании облаков и зон дождя, выяснилось, что фрактальная размерность границ облака (связь периметр-площадь сечения) 1,35±0,05 («изучалось с помощью оцифрованных радарных изображений).
Вот такая «мерность» у «белогривых лошадок»
«… мы говорим не о фактах, мы говорим о той прозрачной истине характеров, чувств, событий на каком-то совершенно другом уровне». (Дина Рубина)
Прочла «Не вычёркивай меня из списка…» Дины Рубиной. В этот сборник вошли две новые повести и рассказы прошлых лет – воспоминания о родных автору людях. Название книги – это сложная ассоциативная перекличка смыслов. Первый связан с праздничным пожеланием, существующим у евреев: «Дай бог, чтобы Всевышний вписал вас в списки «Книги жизни». То есть, чтобы ты был жив в следующем году и год был удачным. И ещё один смысл: мы живы, пока о нас помнят…
Почему нравятся те или иные книги? Я думаю, потому что находишь в них что-то общее с собой, своим восприятием мира, мыслями, эмоциями…
Вспомнилась фраза младшего брата: «Ну ты и игрушечник, папа…» «Игрушечник» в смысле – актёр. Дело в том, что в детстве наши взрослые развлекали нас, детей, без телевизоров и мультиков. Мы с братом любили домашний кукольный и театр теней. Актёрами были наши близкие, иногда и мы сами. Ведущим актёром был наш отец. Он обладал даром перевоплощения, и мог говорить за всех персонажей пьесы сразу. Часто эта игра плавно перетекала в реальную жизнь. Если мы начинали баловаться нас утихомиривал голос волка или голос медведя, объяснявшего, что пора спать и почему сон полезен. За столом тоже иногда разыгрывались целые спектакли с участием лесных жителей, например о том, как полезна тыквенная каша.Все персонажи от зайца до медведя игрались одним актёром – папой.
Вспоминается прекрасное приключение длиной почти в месяц. Я перешла в 9 класс, брат – в 6-й. Отец взял нас в «кругосветное путешествие». Из Грозного во Владикавказ автобусом, далее по военно-грузинской дороге через Крестовый перевал в Тбилиси, частично пешком, частично попутками. Из столицы солнечной Грузии в Батуми поездом, из Батуми в Сухуми лайнером «Россия», из Сухуми в Сочи на катере на подводных крыльях, из Сочи домой самолётом. Во всё время путешествия с нами обязательно присутствовал кто-то четвёртый. В Осетии это была тётушка Марха, которая объясняла нам, что розовую водичку, что подавали с хинкали не пьют, там моют руки, после того как съедят эти большие мешочки из теста с фаршем… Что хинкали не съедают полностью, тот хвостик из теста за который берутся руками эти изделия, оставляют на тарелке: он слишком плотный… По дороге в Тбилиси Марха перерождалась в проводника Гиви, который вообще не реагировал на скулёж типа:«Ну пап, мы устали…» и без устали рассказывал о строительстве военно-грузинской дороги, о Багратионе, о царице Тамаре, об обычаях гор… И откликался только на имя Гиви, как и во Владикавказе только на имя Марха, В Тбилиси на имя Бадри, в Батуми – Самвелл, Сухуми – Сандро… Удивительно как он не забывал вымышленные истории и биографии своих персонажей, иногда хотелось его подловить, «случайно» перепутав события из жизни одного с другим… Но он был великим «игрушечником» и всегда переспрашивал: «Это вы о чём, я такого не помню», или что-то в этом роде… Эта была замечательная игра. Потому что такие «игрушечники» делают нашу жизнь ярче и интереснее.
Иногда я думаю, как правы те психологи, которые говорят, что девочки из хороших семей выбирают себе спутников жизни, похожих на отца. Не специально выбирают, на уровне подкорки. И бывают несчастны, если не встретят хоть чем-то похожего на него в своей жизни.
Конечно важно не перепутать реалии, и не искать всю жизнь двойника отца (это невозможно), но я думаю, если всё-таки такая встреча состоится, это будет счастьем девочки-женщины.
Добрый день!Повезло мне, наконец, сфоткать шествие наших кришнаитов в парке Сосновка.С нынешнего лета начали они ходить по субботам-себя показать, людей посмотреть и привлечь, разумеется, новых адептов.Впереди идут девушки в длинных юбках и машут веерами-а сзади идут парни с шарами и бьют в барабаны, и все поют “Харе Кришна”.Сбоку идет женщина и угощает всех песочным печеньем с красивой ленточкой(а также раздает брошюры).Печенье я взяла-а от брошюр отказалась.Пусть себе ходят-люди они безвредные, а зрелище красивое.Кстати, ленточки от печенья я пристроила на елку-в виде бантиков.Ленточки очень хорошие-красные с золотом.Так что и от кришнаитов польза есть..
Есть какие-то моменты, ничего не значащие, но приносящие просто гигантскую радость. Странные моменты жизни.
Был некий год от Рождества Христова, когда оказался (довелось, пришлось?) на нашем всём – побережье самого любимого и незаменимого, особенно сейчас, самого чёрного в мире моря.
Был месяц март, обосновались мы в санатории «Известий», на самом деле очень удобно до всех точек которых хочется и можется достичь просто пару шагов. И были мы единственными жильцами этого чудного места, которое представляло пятиэтажный колодец с бассейном п центре этого колодца.
Хранительницы этого очага, видимо потрясённые нашим желанием принятия утренних ванн, тут же наполнили бассейн (к утру, само-собой) морской водой, предложили кипяточек! но, конечно, не подогретой водой. «Был месяц март» , напомню.
И утро начиналось так – забег в плавкав со второго этажа, заплыв, по мере замерзания в бассейне, забег скукоженного тела на второй этаж в номер и…, о наслаждение!, горячий, почти кипяток (своя котельная, я полагаю, и не годы оптимизации) душ!
Да, а, вообще-то, чего вдруг вспомянулось? Да так, просто всплыло вдруг в голове. Бывает. И бассейн с ледяной водой и чувал мандаринов из Абхазии, много чего лезет в голову. Прошу прощения за мысли невпопад.
Да, кстати, вдруг вспомнилось. Когда закончились деньги (ТВ Центр» с момента образования, в мае месяце 97-го года, до конца августа денег не платил – слава мэрским героям). Приходилось выживать, но это так, к слову сказать.
Зачем написал? Да хрен знает зачем. Просто вдруг всплыло, всплыло ни кому и ни за чем ненужное, но как-то держащее на плаву воспоминание. Бывает.
После Ковида некоторое время наблюдалась у пульманолога. И в качестве отчёта о ежедневных прогулках к берегу моря приносила ей фото, а потом нарисовала и подарила ей акварель.
Вчера наконец дождалась очереди на УЗИ сердца в диагностическом консультативно-лечебном центре. Понятно, что нервничала несколько дней, а когда поднялась на второй этаж в отделение функциональной диагностики была уже совсем «на взводе». И вот, присев в кресло, увидела на стене напротив свой рисунок. Вначале мелькнула мысль: «Я же доктору подарила, почему он здесь?» А потом огляделась, а там по всему коридору в одинаковых рамочках пейзажи. Улыбнулась: «Вот и мой рисунок попал в Галерею…» 
Вспомнила, как рисовала. Сначала для отчёта фотографировала берег моря. Фотографии не сохранила, только одну оставила. Но загрузить её не получается.Что-то там превышено. Жаль. Увидели бы наше море, непохожее ни на одно другое. Мне эти фотографии потом помогли, когда рисовала свою картинку. А картинка помогла успокоиться перед обследованием. Не очень удачный ракурс, с того места, где ждала вызов. Казалось неудобным подойти и сфотографировать картинку. Боюсь нелепостей. Но очень хотелось показать своим близким, где теперь обитает мой рисунок.
Для меня это стало приятным сюрпризом.
Динамика неравновесных систем – забавная вещь. Даже маятник может стать вверх ногами.
“Для этого я содержу опытных, хорошо оплачиваемых специалистов,
которые могут доказать все, что
угодно… Что люди ходят на руках
и люди ходят на боках.” Дон Рэба
Каких только маятников не бывает. Маятники Максвелла, Ньютона, Обербека и даже простые/математические, которые проходят в школе, говоря о гармонических колебаниях. В математических всё понятно, x~d2x/dt2 и удивляет разве что независимость периода от массы грузика.
А чтобы Вы сказали о перевёрнутом маятнике? Маятнике, у которого грузик устойчиво колеблется в верхнем положении?
В 1951 году, сидючи в опале на Николиной горе, Пётр Леонидович придумал, объяснил механизм работы и собрал такой маятник. (УФН 1951, май или https://ufn.ru/ufn51/ufn51_5/Russian/r515_b.pdf ). На Арнольда это произвело такое впечатление, что он не только написал и порешал соответствующие уравнения, но и не пожалел старой электробритвы, чтобы со второй попытки собрать такой же. Капица скромно написал: «После ознакомления на опыте с динамической устойчивостью маятника в перевёрнутом положении трудно не притти к выводу, что она так же поучительна, как и динамическая устойчивость волчка, и ей также следует занять почётное место в лектории на демонстрациях по механике.». А последняя опубликованная работа Челомея – В. Н. Челомей, Парадоксы в механике, вызываемые вибрациями, Докл. АН СССР, 1983, том 270, № 1, 62–67. У Челомея маятник мог как угодно орииентироваться относительно подвеса + отдельно у него в жидкости всплывали со дна тяжёлые и тонули лёгкие шарики .
Но вернёмся к Капице. Про параметрический резонанс все, кто на качелях качался, знают. Болтаем ногами в такт качелям, вовремя переносим центр тяжести и раскачиваем качели.
У Капицы грузик закреплён на жёстком стержне, эксцентрик вертикально с частотой ω заставляет двигаться точку подвеса, точку О . То что так энергию можно закачать понятно, но откуда устойчивость в верхней точке?
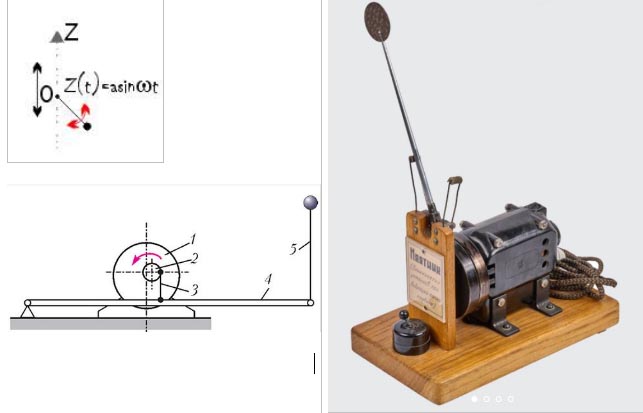
Для начала перейдём в системе отсчёта, в которой точка О неподвижна. В ней на маятник (грузик (подвес невесомый, трения нет)) действует сила инерции. F=−md2z/dt2=mω2z(t)
Теперь посмотрим, что происходит в невесомости (g=0).
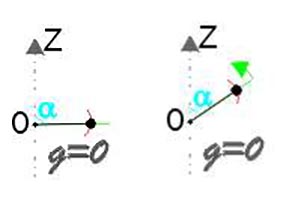
В невесомости направления +Z и – Z равноправны.
Ставим маятник «горизонтально» (рис. слева) и включаем мотор.
За период колебания в среднем на маятник будет действовать одна и та же инерциальная сила, направленная сперва вверх, а затем вниз. Таким образом, маятник будет колебаться лишь перпендикулярно оси движения подвеса, никуда не сдвигаясь (средний момент сил инерции за время колебания подвеса равен нулю, на ½ дуге +Z и на ½ дуге – Z) .
Поэтому, если начальное положение подвеса горизонтально (/2), при запуске мотора в системе координат связанной с О, маятник будет совершать колебания по симметричной дуге (помечена красным).
Пусть теперь начальное положение маятника определяется углом ≠/2 (рис.справа). Для произвольного значения синус несимметричная ф-ция, но тогда, за время одного колебания маятника средний момент сил, вращающих маятник по часовой стрелке, слегка больше, чем момент сил, вращающих против. Из-за этого ось равновесия (зелёная) будет медленно поворачиваться вверх — пока не станет вертикальной. Очевидно, что если бы начальный угол с вертикалью был бы тупой, то ось поворачивалась бы вниз.
Движение маятника, таким образом, можно разделить на две компоненты: быструю и медленную маятник будет быстро колебаться, меняя угол относительно некоторого временного равновесия, которое направлено под углом к вертикали, а сама ось будет из-за нескомпенсированного момента сил поворачиваться, чтобы стать вертикально.
Включение силы тяжести мало что изменит. В каждой точке траектории грузика добавится компонента F=mg, умноженная на синус угла, задающего мгновенное положение оси около которой колеблется маятник. Но, если эта сила (момент силы) будет меньше силы инерции маятник всё равно будет потихоньку подниматься пока не установится в верхнем положении.
При малых углах это даст условие равновесия «кверх ногами»: a2 ω2>2gL
Какая отсюда мораль? Маятник заведомо устойчивая, но неравновесная система. Приложив даже малые усилия, её можно заставить искать новые положения равновесия. Капица предложил свой маятник как модель для исследования режимов работы ускорителя. Похожие решения возникают на рынке при быстро меняющихся спросе/предложении.
«Сказка ложь, да в ней намёк»
PS Сейчас найдены решения, в которых поведение маятника становится хаотическим.
В жизни каждого, вероятно, случались события, которые невозможно объяснить с точки зрения здравого смысла. Такие события, наверное, и называют чудом.
В Грозном было время, когда Дудаев объявил о реформе образования… Всеобщее начальное образование – начальная школа, а затем раздельное образование для девочек, которые переводились на домашнее образование, и для мальчиков образование в военных или религиозных школах. Родители и преподаватели выступили против. Учителя объявили забастовку по-японски, то есть продолжали ходить на работу и добросовестно выполнять свои обязанности. Родители в благодарность брали на себя негласные обязательства поддерживать учителей материально, так как зарплату, по распоряжению властей Ичкерии, учителям не выплачивали. Помогали в основном продуктами. Приходишь на урок, а у тебя на столе стакан сахара, несколько картофелин, головка лука, макароны… Вот когда родительский комитет работал без всякой стимуляции со стороны классного руководителя :)).
Но приходило лето, а с ним каникулы… Каждый устраивался, как мог. Я по приглашению соседки, оставшейся без работы после закрытия завода “Электрон”, и преподавателя химии нашего Нефтяного института вошла третьей в бригаду батраков . Работали в поле. Оплата в конце рабочего дня продукцией. В тот день это были огурцы. Полная самодельная, сшитая из крепкого материала сумка, очень тяжёлая. Машина у хозяина сломалась, и он, дал нам тележку, такую двухколёсную арбу в миниатюре. Идти было не очень далеко. Поле граничило с нашими микрорайонами, и дома были видны на горизонте. Думаю, по времени дорога занимала около получаса.
На полпути к дому нам наперерез вышел человек с автоматом на плече в неадекватном состоянии: то ли обкуренный, то ли обколотый. Тогда часто можно было видеть вооружённых странных людей и не только с калашниковым, даже с “мухой” на плече. Мужчина выстроил нас и сказал, что воров Пророк призывает жестоко наказывать и он сейчас будет нас расстреливать. Мы пытались объясниться, показывая в сторону видневшейся очень далеко хозяйского зелёного жигуля, что мы не воры, а всё, что в наших мешках, заработали честно. Мужчина не слушал, но увидел приближающегося к нам ещё одного рабочего с соседнего поля, на раме велосипеда тот вёз мешок с овощами. Наш “судья” присоединил и его к нашей троице. Повторив ту же речь, взвёл автомат. Евгений Петрович (так звали человека, оказавшегося в одном ряду с нами) сказал нашему встреченному, что он верующий и хочет помолиться перед смертью. Тот разрешил. “Боже, – начал Е.П., – я хотел бы предстать перед тобой очищенным от всей скверны, что накопилась за всю мою жизнь, но ты видишь, что я не успеваю, поэтому прими мою покаянную молитву сейчас…” И он начал исповедоваться, став на колени и время от времени произнося: “Прости, Господи!” В эти моменты мужчина тоже вставал на колени и произносил своё:”Алла!”. Потом, видимо, устав вставать и вновь опускаться на колени, перестал подниматься и начал, как нам показалось, сам молиться, не поднимая головы от земли. А потом мы услышали странные звуки, похожие на храп… Он на самом деле уснул. Е.П. , сделав нам знак рукой – “пошли”, двинулся осторожно дальше по дороге, за ним и мы, прихватив свою тележку с огурцами… Отъехав чуть, бросились бежать, не бросая тележки. Остановились только, выехав на асфальт микрорайона. Вот тогда Е.П. и сказал, что у нас всех сильные Ангелы-хранители, они нас и спасли. Его слова, что силу Ангелы-хранители черпают из наших добрых дел, а с каждым неблаговидным поступком сила и способность к нашему спасению у них уменьшаются, запомнились мне навсегда.
Вот и прагматический вектор жизни, делай добро, чтобы Ангел мог спасти тебя в тяжёлые минуты 🙂
Хотя это не шутка. Но, вероятно, и не доказательство. Но я не могу объяснить случившееся тогда с нами иначе, чем вмешательством Бога и Ангела в наши жизни.
Таганрог – настоящий южный город, визитная карточка которого – доброжелательность и открытость.
В статье «Родом из провинции. Город Чехова» у меня есть мысль: «В небольшом городе историческая память имеет крупный план». Написала, имея в виду своеобразный исторический палимпсест. Когда в художественном полотне сквозь слой краски видишь другую, ранее написанную, картину, – это называется палимпсест. Так в историческом палимпсесте сквозь время в настоящем просвечивают события дней минувших.
О Великой Отечественной войне в Таганроге помнят всегда и Бессмертный полк таганрожцев – не только сражавшиеся с фашизмом на поле боя. Мало кто знает, что в нашем городе была своя «Молодая гвардия», свои герои, казнённые за сопротивление оккупантам. Младшему из них было всего 12 лет. Их родные и близкие живут рядом, бережно хранят память о них и не дают прорасти беспамятству в душах земляков в наше время.
Нужно ли говорить о том, что отношение к тому, что происходит сейчас на СВО у таганрожцев особое? В них по-прежнему нет «той агрессивности, безразличия, какими жители мегаполисов защищают своё пространство», здесь по-прежнему «не чувствуешь себя чужим». Поэтому многие, кто попадал в наш город во время СВО по случаю, мечтает вернуться сюда «если судьба оставит в живых», чтобы жить здесь постоянно. Добродушие, искренняя заинтересованность в другом человеке, сочувствие, сострадание – эти черты характера жителей нашего города не могут не привлекать. Но бросается в глаза и то, что характер города стал неоднородным.
Вот картинка из отделения Сбербанка. Очередь. Много беженцев (на получение пособия очередь – отдельная, кстати). Входит дама и, ни к кому конкретно не обращаясь, начинает громко возмущаться тем, что не может оплатить квитанции уже несколько дней, так как в зале не протолкнёшься. Никакие объяснения её не устраивают и не успокаивают. Проще уж обратиться к беженцам и сказать им, чтобы не смущались, напомнить чеховскую фразу о воспитании, чтобы разрядить обстановку. Не разряжается: какая-то бабулька-таганроженка обозвала даму фашисткой…
Нет, такие картинки не часты. Вот ещё одна. Сижу на автобусной остановке. Электронное табло показывает, что мой автобус только что ушёл … Ждать нужно будет 18 минут. Несколько в стороне молодой мужчина в инвалидной коляске, без ног. У него такой взгляд, повёрнутый во внутрь, что хочется подойти и спросить о чём-нибудь, глупость даже какую-либо, всё равно что, лишь бы не оставлять его с этим взглядом «во внутрь» наедине. Пока придумывала, что спросить: про аптеку или магазин «Эльдорадо» (он прям напротив, с огромной вывеской) – к нему подпорхнула молодая женщина, чмокнула в щеку, бросила: «Заждался?» И о! чудо! Его как будто солнечным светом облили. Заулыбался, взгляд ясный, лицо светится изнутри… Так приятно смотреть на них. Развернулись и медленно покатили по аллейке о чём-то переговариваясь, женщина при этом время от времени слегка склонившись заглядывала ему в лицо, смеялась… Всё побеждает любовь…
Вот всё думаю, сможет ли она победить разобщённость, что неизбежно возникает среди некоторой части людей, кто сейчас находится по разные стороны этого безумия? И что нужно для того, чтобы люди радовались друг другу, как эти двое с автобусной остановки?
Разговоры по душам.
Помню забавный рассказ в таганрогском альманахе молодых авторов «У солнечных часов» о странном ангеле. Сюжет простой: автор-рассказчик по дороге в булочную встречается с ангелом, который невзначай сообщает ему, что прохожий, идущий им навстречу, решился на самоубийство. Автор в ужасе: «Сделай же что-нибудь!» Ангел произносит устало: «Почему люди считают, что мы им что-то должны?» – но тем не менее помогает! Очень своеобразно помогает: ошалевшему прохожему вкладывает в руку пистолет «Держите, вот то, что Вам сейчас нужно.Надеюсь, одного патрона Вам хватит?» Рассказчик в панике бросается к прохожему, чтобы как-то помешать ему, и видит краем глаза, что ангел подошёл в это время к полицейскому и что-то тому сказал. Прохожего арестовывают за незаконное хранение оружия.
Автор-рассказчик в полном недоумении и растерянности.
« А Вы чего же ждали?- спрашивает его Ангел. – Ну потрачу я время на уговоры, буду убеждать, что жизнь прекрасна, что её может забрать только Бог, что возвращения с того света не может быть в принципе, и что… Но не факт, что уговорю. А так в ближайшие полгода до суда ему будет не до самоубийства. Да и год условно пролетит незаметно. И в этот год ему будет не до того, чтобы обдумывать способ ухода из жизни».
Странный ангел?
Мне кажется нет. У них, у ангелов своя логика, своё видение наших проблем. И потом… Действительно, а почему мы считаем, что они нам что-то должны?
Изучая Закон Всемирного Тяготения по любимому Пёрышкину, задал себе вопрос – а откуда Ньютон знал расстояние до Луны?
Квадрат расстояния в знаменатель он написал, зная отношение ускорений яблока и Луны на орбите
Период обращения Луны он знал. А расстояние откуда?
Оказалось от греков. А греки умели измерять такие расстояния голыми руками за 300 лет до н.э. (это сейчас просто – установил уголковый отражатель на Луне. а на Земле включил лазер).
Начал Эратосфен с измерения радиуса (длины по меридиану) Земли. В Ассуане Солнце в полдень (22 июня?) было видно из колодца (значит точно в зените), а в Александрии под углом 7.2 градуса. Зная расстояние Ассуан-Александрия можно было найти радиус Земли.
И ничего, что Ассуан не строго на юге, а расстояние оценивалось по средней скорости верблюжих караванов, во времена Колумба/Магеллана это была лучшая оценка (сейчас 6356-6378, т.к. не шар, а геоид).
Далее Аристарх Самосский сообразил. что в первой/последней четверти угол Солнце-Луна-Земля — прямой и посчитал отношение расстояний от Земли до Луны и Солнца (угол Солнце=Земля-Луна измерялся).
Любопытно. что понятие косинуса не было, но подобный по углу треугольник он построил.
С отношением размеров Солнца и Луны просто повезло. Солнечные затмения видны в узкой полосе и недолго. Значит размеры соотносятся как расстояния.
Последний шаг – тень Земли на Луне. Зная видимую длину дуги тени Земли оцениваем радиус Луны, а потом используем все имеющиеся уже отношения расстояний.
Измерение тени у меня вызывает просто щенячий восторг. Через 15 веков это делали с подзорной трубой (телескопом) так:
Тоже не просто. Успеть нарисовать движущуюся Луну, потом на ней тень Земли я бы не смог. Сфоткал бы, на ПЗС матрицу и не торопясь строил окружность по дуге. Но у греков и трубы не было!
Скорее всего у Ньютона в показатели степени получалась не совсем двойка, а греков я зауважал ещё читая “Занмательную Грецию” М.Гаспарова, но столь блестящих результатов от племени философов я не ждал
Доброе утро!На-днях, гуляя по нашему парку Сосновка, увидела вот такую картину-“одетое дерево”.Кто-то, видимо, навязал полосы из остатков пряжи- и украсил дерево подобным образом.Поспешила сфоткать редкую картинку-и поделиться с вами.И вовремя-на следующий день прохожу, а красоты уже нет.Народ приватизировал в свою пользу-для этого, видимо, автор и старался.Ну, хоть не пропало добро-все равно бы размокло под дождем.И то ладно..
Добрый день!Сегодня, гуляя по парку-встретила трухлявую березу, сплошь покрытую внизу кольцом опят.В нашем парке эти грибы не редкость-водятся на трухлявых пнях.Но сейчас октябрь-обычно опята уже заканчиваются к этому времени.А тут сентябрь теплым был, и дожди пошли-вот они и вылезли..К сожалению, сама не ем- а показать было некому, шел дождь.Надеюсь, грибы найдут-опята быстро перерастают и становятся невкусными.Там можно было снять с дерева килограмм, не меньше.Прошу прощения за качество снимка-снимала хоть новым мобильником, но камера неважная(старый смартфон приказал долго жить).Захотелось с вами поделиться редким кадром-ведь скоро холода и конец грибного сезона..
Доброе утро!Нет, я не оговорилась-вчера наступил Новый год по еврейскому календарю.Поскольку отсчитывается он не от рождества Христова, а от сотворения мира-то наступил 5784-й год.Еврейский новый год отсчитывается по лунному календарю-поэтому дата его “плавает” по сентябрю.В Новый год и десять последующих дней принято каяться в грехах и просить прощения у близких и Бога-чтобы он оставил вас в числе живущих.Подают на стол обязательно мед(чтобы год был сладким), гранаты или яблоки, рыбу обязательно с головой(название праздника на иврите “Рош-ха-шана” означает “голова года”),а еще морковь(ее нарезанные кружочки символизируют золотые монеты) и сладкую булку халу.
Памятуя, что все мы произошли от Адама и Евы(или общих животных предков)-приглашаю присоединиться к празднику.Счастливого и сладкого Нового года!
