Размышляя над итогами экспедиции адмирала Чжун Хэ (и Васко да Гама) я дошёл до пифагорейцев. Революционной идеи, что миром правят числа и законы управления познаваемы. Возможно я не в теме, но похоже ничего подобного вне Европы сформулировано не было. И, видимо, здесь и разошлись, через много поколений, судьбы развития Европы и всего остального мира. Европа пошла по скользкому пути научно-технической революции, т. е. занялась внедрением познаваемых законов природы и их утилизацией.
Толком не зная науки о числах, я весьма впечатлён результатами математического моделирования. Я даже не о Ньютоне-Максвелле-Эйнштейне, я о простеньких моделях типа роли зависти. С возникновением возможности компьютерного моделирования математические модели стали сложнее, но нагляднее, а результаты становятся всё чудесатее. Сказка ложь, да в ней намёк…
Клеточные автоматы. В игру «Жизнь» не играли? Очень поучительно. Листок бумаги в клетку (на мониторе). Клетка может быть белой(пустой) или чёрной (живой). Всего соседей 8. Если есть 2 или 3 живых соседа, клетка выживает; если меньше 2 — погибает от одиночества, если больше 3 – гибнет от перенаселенности; если у пустой ровно 3 соседа – рождается новая клетка. Ещё граничные условия циклические. Проще правил и не придумаешь. Меня завораживали картинки эволюции вводимых «зародышей», определённых такими простыми правилами. Примеры на маленьком поле
Первоначально идея клеточных автоматов возникла при разработке самовоспроизводящихся систем (робот собирает робота). Первое практическое применение – распространение импульса в сердечных нервных узлах (аритмия). Пошли автоматы и в криптографию, и в рекресталлизацию.
Но нашлось и ещё одно применение. Программисты люди простые. Закономерно возникла идея – а наблюдаемая Вселенная не является ли клеточным автоматом? Стивен Вольфрам продвинулся по этому пути достаточно далеко. Ему удалось выделить класс автоматов (правил), в которой возникают локальные устойчивые структуры. Его мир принципиально дискретен (и в пространстве, и во времени). Шаг дискретизации мелок настолько, что мы этого не замечаем. Правила недостаточно просты, чтобы мы могли рассчитать эволюцию системы быстрее, чем происходит эта эволюция (здесь аналогия с газовыми законами; посчитать макроскопические параметры мы можем, но не через законы движения отдельных атомов. «мы не можем даже приблизиться по количеству выполняемых итераций к тому числу итераций, которое произвела наша Вселенная с начала своего существования“). Тем не менее, пространство можно представить как результат развития минимального количества (трех узлов), связанных простым правилом за конечное число итераций («И я думаю, что именно так устроено все пространство в нашей Вселенной. В общем-то это куча дискретных, абстрактных отношений между абстрактными точками. Но при взгляде с определенного масштаба мы видим, что паттерн этих отношений делает эту структуру похожей на привычное нам непрерывное пространство. Это похоже на наше представление о воде: по сути вода — это куча дискретных молекул, но когда мы смотрим на нее с большого масштаба, она кажется нам непрерывной жидкостью.»). В этом построении какой-нибудь электрон может быть просто свойством узла гиперграфа.
Очевидно, что введённые правила задают и кривизну пространства, а значит и геодезические линии (не непрерывные, соединяющие узлы).
Возникает понятие причинно-следственной инвариантности (от исходной конфигурации можно прийти к конечной по разным путям)
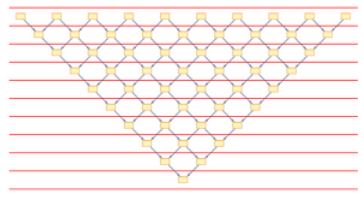
(развитие простейшей итерации)
Возникает время – интервал между циклами итераций. Оно необратимо, распутать этот клубок не получается. Возникает преобразование Лоренца ( точнее √(1-β²), поскольку, «стоя» мы движемся на рис вертикально, а «на бегу» наклоняяем ось времени. Только откуда взялась именно скорость света я не понял).
Возникает естественным образом импульс, энергия и даже E=mc² . Много всего. В совершенно незнакомой мне математике. И что существенно, нет противоречий с существующей уже крупномасштабной картиной мира.
Я это воспринимаю, как и инфляцию, по Гегелю, – «всё разумное – действительно». Изумительно красивое построение, которое возможно имеет отношение к реальному миру.
Имеет ли это отношение к нашей Вселенной? Бог весть. Существенно, что от Пифагора, Васко да Гама…, ошибаясь и спотыкаясь, человечество строит картину мира от масштабов, где ничего нельзя уже «пощупать» до расстояний, где уже почти ничего не видно. Пытается осознать события происходящие от 10⁻⁴⁴ секунды до 14 млрд лет.
Ссылку на статью я дал. Желающие могут раскрутить.
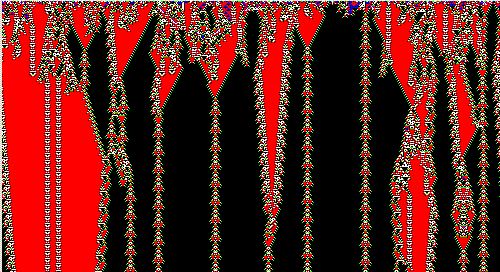

Мда, Андрей..Почти по Чехову:”Кто писал-я знаю, но ничего не понимаю”. Может, до остальных доходит лучше, чем до меня..Можно, конечно, представлять разные красивые математические модели-но вот имеют ли они отношение к реальности?Кто знает..
Выглядит непротиворкчиво. Может и так, а может не так! Есть над чем подумать. Спасибо!