Рубрика: Физика

На Ютубе как-то показывали научно-популярный фильм из серии “Через червоточину с Морганом Фриманом”. Там показывали как проводится двухщелевой опыт Юнга над отдельными частицами. Это парадоксально, но оказывается точечная частица может пройти через две щели одновременно, оставляя при этом на экране интерференционную картину.

Ещё парадоксальнее оказывается тот факт, что если детекторы частиц будут расположены на щелях, показывая через какую щель проходит электрон, интерференционная картина исчезает. Детектор при измерении коллапсирует волновую функцию электрона. Определившийся (детерминированный электрон), в отличие от волнового, не может создать интерференцию с самим собой.

Теперь моя идея. Допустим, мы собрались передать некую последовательность нулей и единиц с Земли на Альфу Центавра. На полпути между Землёй и Альфа, на космическом корабле находится источник запутанных частиц, выдающий пакеты по 50 электронов, направленные в противоположные стороны.

Волновая функция двух запутанных электронов общая. Коллапс единой волновой функции происходит мгновенно по всему пространству Вселенной, независимо от текущего расстояния между ними. Это и следует использовать.

На Земле мы подвергаем взаимодействию первые 50 электронов, например с помощью фотопластинки. При этом попарно схлопываются общие волновые функции электронов, находящихся на Земле и на Альфе. Все электроны первого пакета, и там и там, утратят свою волновую функцию и окажутся в определённом состоянии. Альфовцам следует пропустить первый пакет через две щели по методу Юнга по одному, исключив возможность прохождения через щели двух и более электронов за раз. Определившие электроны, не могут пройти через две щели одновременно и создать интерференционную картину. На выходе альфовцы получат рисунок двух щелей. Значит – логическая единица.

Второй пакет электронов на Земле не трогаем вообще, а пропускаем мимо в свободный полёт. Альфовцы пропускают второй пакет через две щели. Волновой неопределившийся  электрон, может пройти через две щели одновременно и создать интерференционную картину. Я думаю что используя 50 электронов, визуально различить рисунок двух щелей от интерференции можно точно. В случае интерференции – логический ноль.

Итого, с помощью 1000 запутанных пар электронов можно передать 20 бит информации почти мгновенно.

Через несколько лет после смерти Эйнштейна и Бора, их спор продолжили другие учёные. Интуитивно казалось, что возможность или невозможность существования скрытых параметров до измерения, подтвердить или опровергнуть невозможно вообще никаким способом, однако решение было найдено.

Крайне упрощённо это можно представить так. Вы захотели проверить теорию скрытых параметров. Допустим у Вас есть друг – картёжник и шулер, с которым Вы решили сыграть в игру с угадыванием цвета карты.

Вы говорите – красная, а он с закрытыми глазами выкладывает чёрную. Он выиграл. Вы говорите – чёрная, а он выкладывает красную. Снова он выиграл и т.д.

Вы интересуетесь: “А как так вообще получается? А он в ответ: “Да у меня карты такие квантово-запутанные, у них всегда цвет противоположный выбору”. Как проверить его заявление? Может он суперфокусник?

Вы предлагаете сыграть в другую игру, с отложенным выбором, где он сначала будет выкладывать карту, а потом Вы делаете выбор. В итоге возможны такие результаты:
1) Если он всё равно будет продолжать выигрывать, значит у него запутанные карты, определённого цвета карты до момента переворачивания не существует.
2) Если Вы будете угадывать 50 на 50, значит карты нормальные, а возможность фокусов исключена.

Обратите внимание, что в первом и втором случае выполняются разные соотношения вероятностей.

Один из двух похожих вариантов будет выполняться и при измерении параметров квантовых частиц. Если квантовая запутанность по Бору существует, то будет выполняться одно соотношение, если же существуют скрытые параметры по Эйнштейну, то другое соотношение.

В 1964 году Джон Стюарт Белл вывел свои неравенства Белла, предложил свой вариант установки с запутанными частицами и точно вывел соотношение вероятностей – в одном случае не более 2:3, а в другом – не менее 3:4.

В 1964 году технологические возможности не позволяли сконструировать такую установку.

В 1972 году Джон Клаузер был сторонником теории скрытых параметров Эйнштейна и категорически не принимал вероятностную трактовку. Найдя в библиотеке работы Белла, аспирант Клаузер, совместно с помощниками смог сконструировать такую установку. Первые же результаты повергли его в шок. Скрытых параметров не было, поведение частиц было принципиально вероятностным по Бору. Первая мысль Клаузера была такой: «Что же я сделал неправильно?  Наверное не достиг требуемой точности». Вторая установка давала большую точность, но в итоге дала те же результаты.

Однако не все учёные полностью согласились с трактовкой результатов эксперимента.

В 1982 году Ален Аспэ провёл более сложный и более точный эксперимент, но всё равно в результате выяснил нарушение неравенств Белла, правоту Бора и заблуждение Эйнштейна.

В 1998 году Антон Цайлингер провёл ещё более сложный и ещё более точный эксперимент. И в результате снова Бор оказался прав, а Эйнштейн нет.

Сторонники теории скрытых параметров предложили модифицированные теории, чтобы хоть как-то спасти концепцию локального реализма. Эксперименты по проверке теории скрытых параметров, учитывающие эти модификации, идут до сих пор, и в результате медленно но верно становится понятным, что локальный реализм и любые теории скрытых параметров на микроуровне не работают. Поведение частиц принципиально вероятностно и непредсказуемо. Частицы не обладают физическими параметрами до измерения. Бор был прав, а Эйнштейн был неправ.

4 октября 2022 года Шведская королевская академия наук решила присудить Нобелевскую премию по физике 2022 года Алену Аспе, Джону Клаузеру и Антону Цайлингеру  «за эксперименты с запутанными фотонами, установление нарушения неравенства Белла и новаторскую квантовую информатику».

Бор и Эйнштейн поднимали в своих спорах совсем не праздные вопросы. Правильные подтверждённые ответы на их вопросы позволяют гораздо лучше использовать квантовые явления для практического применения. Уже подтверждена и успешно работает квантовая телепортация, уже есть квантовые процессоры.

У Нильса Бора и Альберта Эйнштейна было несколько споров на тему странного мира квантовой механики. Это касалось принципа неопределённости Гейзенберга, квантовой запутанности, ЭПР парадокса. И Бор и Эйнштейн, признавали правильность физических формул. Все противоречия касались исключительно интерпретаций, описаний квантово-механических явлений.

До появления квантовой механики самой очевидной истиной в физике считался локальный реализм. Любое тело или частица, существует в определённый момент времени в определённом месте, независимо от того, наблюдают за ним сейчас или нет. Даже в самой запутанной на тот момент, но в то же время проверенной физической теории – теории относительности Эйнштейна, локальный реализм выполнялся чётко.

Ситуация изменилась с появлением принципа неопределённости Гейзенберга – У частицы не могут быть одновременно точно измерены положение и скорость (импульс). Точность измерения подчиняется математическому выражению ΔХ*ΔР ≥ h/2, где h – постоянная величина, приведённая постоянная Планка.

Эйнштейн, всегда стремившийся к максимальной точности и законченности физических теорий, не мог просто так принять этот абсурд, и поэтому придумал свой способ обойти принцип неопределённости. Бор, внимательно изучив мысленный эксперимент Эйнштейна, пришёл к выводу, что Эйнштейн не учёл одну очень важную деталь, и таким образом забраковал его идею.

По мере развития квантовой механики, её абсурдность с точки зрения здравого смысла росла. Бор и другие учёные усомнились в концепции локального реализма, краеугольного камня всех существующих на тот момент физических теорий.
В интерпретации Бора, частицы и их параметры не существовали до измерения, они приобретали реальность и обретали свои параметры исключительно в момент измерения. Эйнштейн отмёл этот абсурд фразой: “Я уверен, что Луна существует даже тогда, когда я на неё не смотрю”.

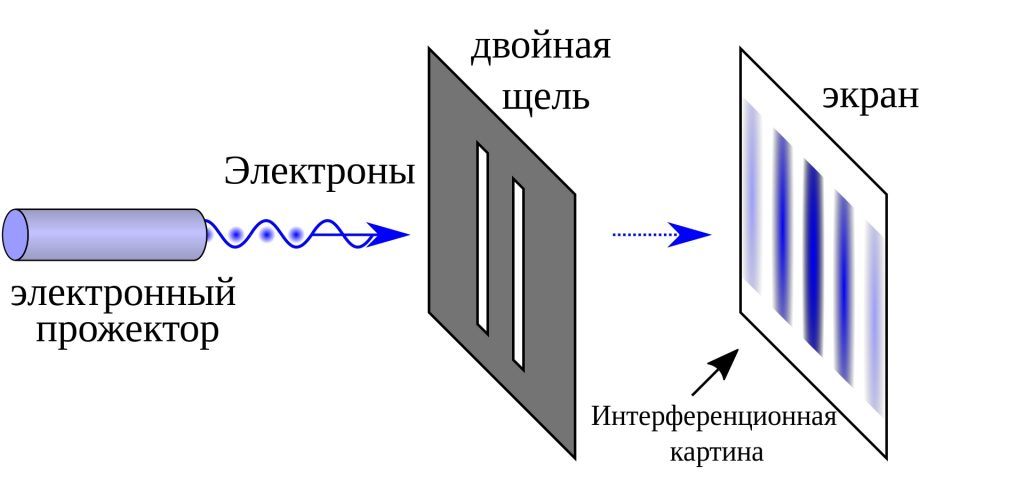
В 1926 году Эрвин Шредингер вывел своё уравнение, в котором фигурировала волновая функция, задающая плотность вероятности обнаружения частицы в определённом месте.

Бор и другие учёные, интерпретировали поведение частицы как принципиально вероятностное и непредсказуемое. В дальнейшем это было сформулировано в Копенгагенской интерпретации:
Волновая функция (вектор состояния) следует унитарной эволюции во времени, описываемой уравнением Шредингера.
Физическим смыслом волновой функции является амплитуда вероятности, квадрат которой есть вероятность обнаружить систему при измерении в определенном состоянии.
При измерении функция «коллапсирует», то есть сосредотачивается в точке, соответствующей результату измерения. Вся остальная информация об исходной функции теряется.

Эта интерпретация вообще не объясняла ничего, а только ещё больше всех запутывала. Эйнштейн как стойкий приверженец более простых объяснений ответил Бору: «Я уверен, что Бог не играет в кости”. Другими словами: “Если мы чего-то не можем предсказать, то это не значит, что в природе также непредсказуемо всё происходит”. Бор, очевидно не понявший глубинного смысла фразы, ответил: «Эйнштейн, не указывайте Богу, что ему делать».

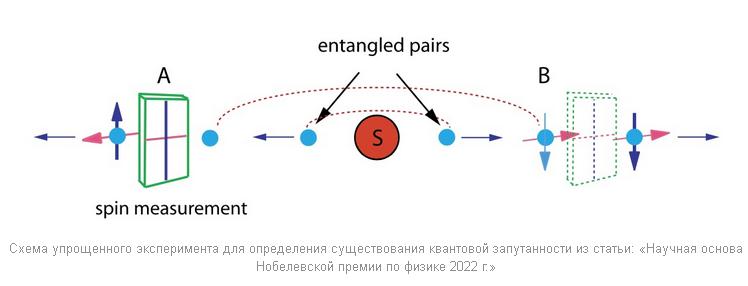
Дальнейшее развитие спора произошло после открытия явления квантовой запутанности. Физические параметры частиц, имеющих общее происхождение, оказываются взаимозависимыми. Например, если при измерении спина одной частицы её спиральность оказывается положительной, то спиральность второй оказывается отрицательной и наоборот. Такая взаимозависимость сохраняется, даже если эти объекты разнесены в пространстве за пределы любых известных взаимодействий.

Эти факты следовало как-то объяснить. Бор продолжал настаивать на принципиально вероятностном поведении частиц. Эйнштейн заметил, что из интерпретации Бора следует сверхсветовая скорость передачи взаимодействий, что противоречило бы его теории относительности. Эйнштейн, совместно с другими учёными, предложил ещё один мысленный эксперимент, который в случае подтверждения опровергал бы и концепции Бора, и заодно принцип неопределённости. Парадокс Эйнштейна – Подольского – Розена:

Допустим, две одинаковые частицы b и c образовались в результате распада третьей частицы a. В этом случае, по закону сохранения импульса, их суммарный импульс должен быть равен  исходному импульсу третьей частицы, то есть импульсы двух частиц должны быть связаны. Это даёт возможность измерить импульс одной частицы b и по закону сохранения импульса рассчитать импульс второй c, не внося в её движение никаких возмущений. Теперь, измерив координату второй частицы, можно получить для этой частицы значения двух неизмеримых одновременно величин, что по законам квантовой механики невозможно.

Исходя из этого, можно было бы заключить, что соотношение неопределённостей не является абсолютным, а законы квантовой механики являются неполными и должны быть в будущем уточнены.

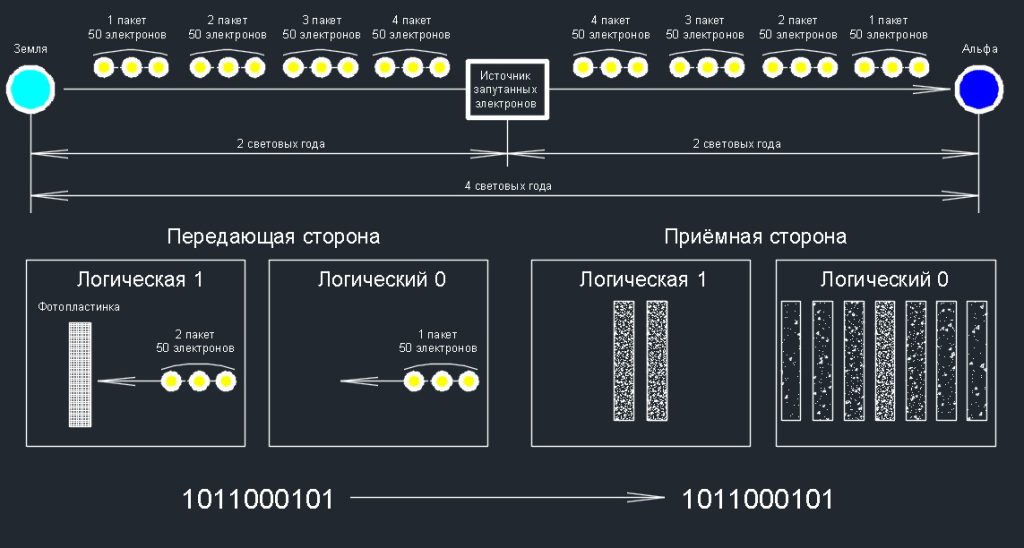
Ответ Бора по сути был примерно таким. Принцип неопределённости и уравнение Шредингера для запутанных частиц обязаны соблюдаться на любых расстояниях. Следовательно, внося возмущения в состояние при измерении первой частицы, мы вносим возмущения в состояния и второй частицы тоже. При этом взаимодействие (или нечто другое) передаётся со скоростью выше скорости света. Передать информацию именно таким способом не получится. Полученные значения для одной из частиц будут принципиально вероятностны. Следовательно это не противоречит теории относительности.

В современной наглядной интерпретации в лучших традициях Моргана Фримана, это выглядит примерно так:

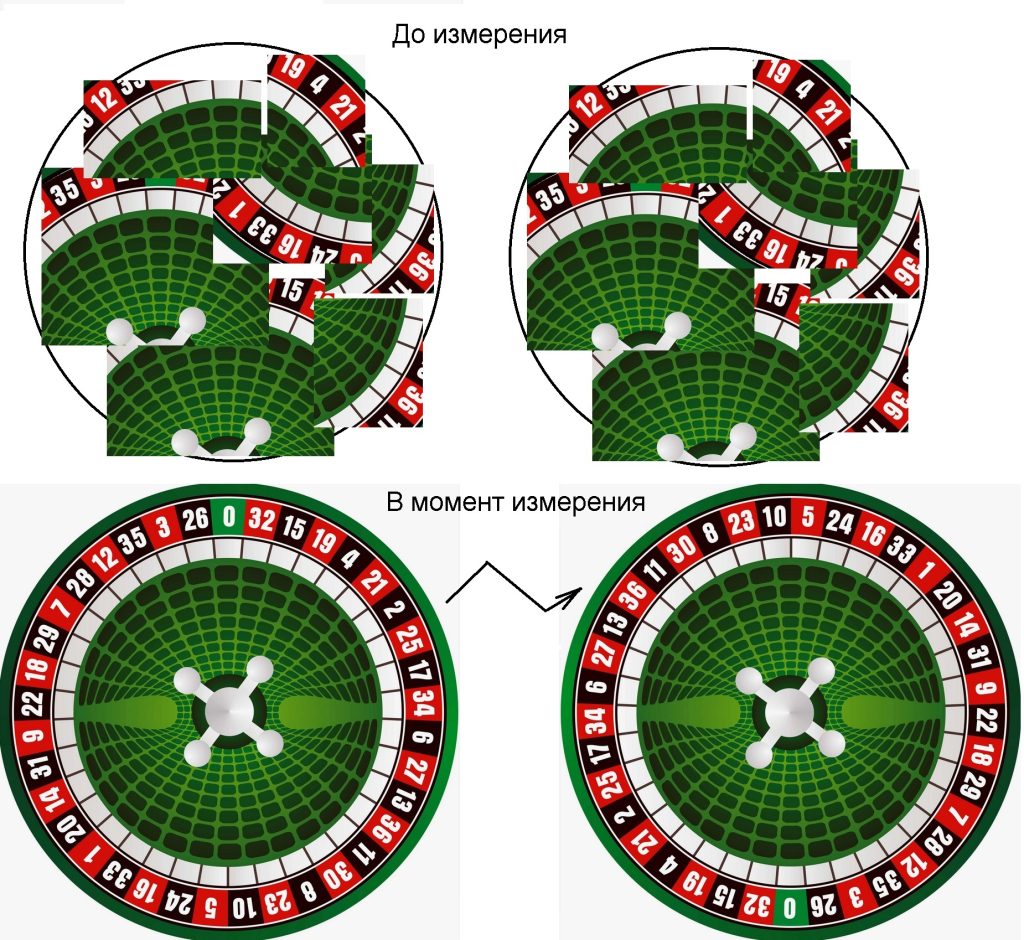
До проведения измерения, запутанные частицы одновременно находятся во всех возможных состояниях, т.н. суперпозиции состояний, подобно вращающейся игровой рулетке. Пока она не остановилась, она обладает одновременно всеми возможными состояниями. В момент измерения происходит коллапс волновой функции, мгновенно во всём окружающем пространстве (призрачное дальнодействие) и частицы-рулетки оказываются в полностью противоположных состояниях.

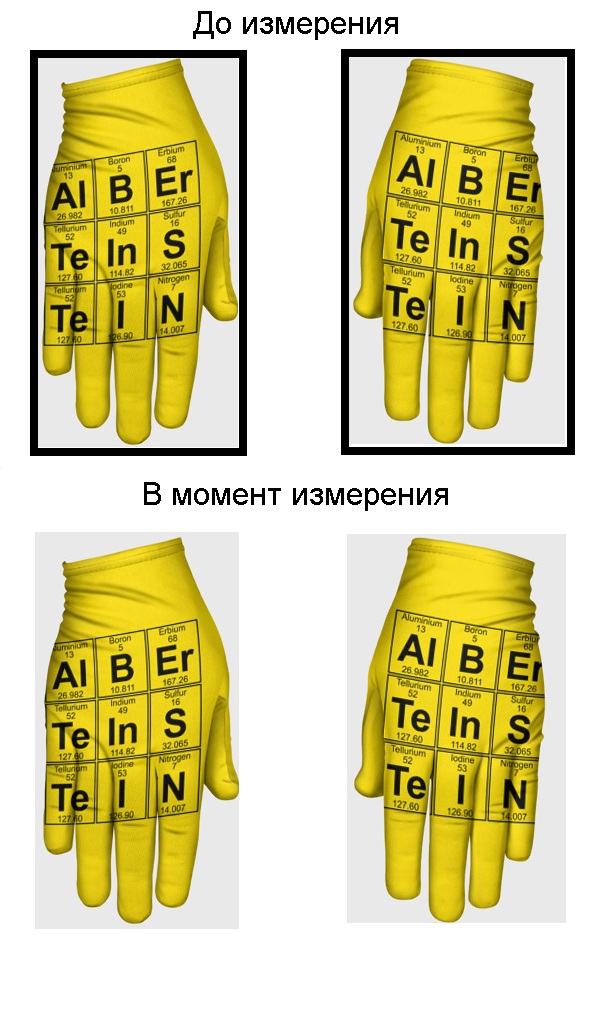
Эйнштейн, как сторонник бритвы Оккама, предложил более простое объяснение этого явления. Запутанные частицы, имеющие общее происхождение, подобны паре перчаток. Они изначально «рождаются» инверсными, или правыми или левыми, и всегда ими остаются. Доставая перчатки из ящиков, разнесённых на миллионы километров, они также остаются или левыми или правыми. Никакого переноса информации при этом не происходит.

После таких аргументов, и Эйнштейну и Бору казалось, что и ту и другую интерпретацию экспериментально проверить невозможно. Экспериментальная физика может лишь показать данные результата измерения, но никогда не сможет дать ответы на то, что происходит с частицами до измерения. Интерпретации перешли в философскую плоскость.

Эйнштейн умер в 1955 году полностью убеждённым в неполноте квантовой механики и абсурдности волновой интерпретации. Бор умер в 1962 году, также оставшись при своём аргументированном мнении.

Как оказалось гораздо позже, и ту и другую интерпретацию экспериментально проверить всё таки можно. Об этом я напишу в следующей статье.

На сегодняшний день не существует единого общепринятого определения времени. Только по этой причине, разные люди вкладывают в этого понятие самый разный смысл.
Вот примеры, которые мне известны:

1) Математическое время, как ось координат t на графике.

2) Математическое время как длительность Δt, между началом и концом события, описанная в публикации Василия Пупкина «Что такое время?»

3) В теории относительности время рассматривается как часть единого физического материального  4-мерного пространства-времени. Как я уже писал в предыдущей публикации, любое тело находящееся в состоянии пространственного покоя, перемещается по оси времени со скоростью света 300000 километров в секунду.

Поскольку оно едино, то на пространство и время должно распространяться единое определение. Как говорил Морган Фриман в одной из своих передач из цикла «Сквозь кротовую нору»: «Пространство-время – эта та часть Вселенной, которая не даёт произойти всему и сразу и упорядочивает события от причины к следствию».

Далее так называемые стрелы времени. Принципиальные отличия прошлого от будущего. В них рассматривается не само понятие время, а как оно изменяется, говоря по-простому – течёт только в одном направлении.

4) Космологическая стрела времени. Вселенная с течением времени расширяется, а не сжимается.
Для объяснения этого феномена выдвинута гипотеза, что пространство-время ранней Вселенной уже содержало в себе всю необходимую энергию для последующего расширения. Подобно заведённой часовой пружине, предоставленной самой себе, потенциальная энергия медленно, но верно переходит в энергию движения.

5) Термодинамическая стрела времени. Во Вселенной с течением времени растёт хаос, частицы занимают более вероятные хаотические состояния

Для объяснения этого феномена выдвинута гипотеза о том, что термодинамическая стрела времени, является следствием космологической стрелы. Введено понятие энтропии, как меры хаоса. S = k*lnW, где k – постоянная Больцмана, W – статистический вес состояния, то есть количество способов реализации данного состояния системы. Поскольку при расширении Вселенной, её объём увеличивается, ничего удивительного что и мера её беспорядка также увеличивается.

6) Квантовая стрела времени. В микромире работает так называемый корпускулярно волновой дуализм. Любая частица до проведения измерения присутствует в нескольких местах одновременно, но с разной вероятностью обнаружения. Но в момент проведения измерения наступает коллапс волновой функции. Частица оказывается в определённом месте в определённое время. После этого такая определившая частица, не может самопроизвольно снова стать волной.

7) Психологическая стрела времени. Мы помним прошлое, но не помним будущее.

Стивен Хокинг в одной из своих книг, путём сложных расчётов показал, что психологическая стрела времени всегда совпадает по направлению с термодинамической и является её следствием. Это справедливо и для живых существ и для неживых, например компьютеров. Любой процесс записи информации в память и считывания её из памяти, обязательно требует энергетических затрат.

Все 7 приведённых примеров показывают, что изначально выбираемые определения  у разных людей разные. В зависимости от этого разные люди, в спорах относительно реальности времени, занимают принципиально разные позиции, довольно часто путая само понятие времени и его течение. Разница в этих двух случаях будет примерно такая же, как между длиной и расширением пространства.

“Представим себе мальчишку, пусть его зовут Несносный Деннис, у которого есть кубики, которые совершенно невозможно разломать и разделить на части. Все кубики полностью одинаковые. Пусть у него, скажем, 28 кубиков. Утром мама оставляет его в комнате с этими 28 кубиками. Вечером она из любопытства тщательно пересчитывает кубики и открывает удивительный закон: что бы он ни делал с кубиками, их число всегда остается равным 28!Так продолжается в течение нескольких дней, пока однажды она не обнаруживает, что кубиков только 27; правда, небольшое расследование показывает, что один кубик оказался под ковром. Ей приходится заглядывать повсюду, чтобы удостовериться, что число кубиков не изменилось. Но однажды количество кубиков все-таки меняется: их оказывается только 26. Тщательное расследование показывает, что в комнате открыто окно; выглянув наружу, она находит два недостающих кубика. Но в другой раз подсчет показывает, что кубиков 30!Это вызывает заметное смятение, пока не выясняется, что в гости со своими кубиками приходил Брюс. Уходя, он оставил два из них у Денниса. Избавившись от лишних кубиков, мама запирает окно и больше не пускает Брюса. Все снова идет хорошо до того момента, когда, пересчитывая кубики, она не выясняет, что их 25. Правда, в комнате имеется коробка  – ящик для игрушек  – и мама собирается ее открыть, но мальчик говорит ей: «Нет, не открывай коробку!» – и начинает реветь. Маме нельзя открывать коробку. Но необычайно любопытная и довольно изобретательная мама разрабатывает план! Она знает, что кубик весит три унции, поэтому она взвешивает коробку, когда на месте все 28 кубиков, и получает вес, равный 16 унциям. Устраивая проверку в следующий раз, она снова взвешивает коробку, вычитает из веса 16 унций и делит результат на три. Она приходит к открытию, что

В дальнейшем снова наблюдаются некоторые отклонения, но внимательное исследование показывает, что меняется уровень грязной воды в ванной. Ребенок бросает кубики в воду, а маме не видно их в грязной воде. Но она узнает, сколько кубиков находится в воде, добавив к своей формуле еще одно слагаемое. Поскольку исходный уровень воды равен шести дюймам, а каждый кубик поднимает воду на четверть дюйма, новая формула получается такой:

По мере постепенного возрастания сложности мира она открывает целый ряд слагаемых, представляющих собой способы вычисления количества кубиков в тех местах, куда ей не заглянуть. В результате она получает сложную формулу  – величину, которую ей нужно подсчитать и которая в ее ситуации всегда остается одной и той же.

Какова здесь аналогия с сохранением энергии?Главный аспект, в отношении которого от этой истории следует абстрагироваться, состоит в том, что никаких кубиков нет. Стоит только убрать первые слагаемые в [двух выписанных выше] формулах, как окажется, что вы вычисляете более-менее абстрактные вещи. Аналогичны же вот какие моменты. Во-первых, когда мы вычисляем энергию, часть ее иногда покидает систему и уходит, а иногда какая-то энергия в систему поступает. Чтобы удостовериться в сохранении энергии, следует проявлять аккуратность в том, чтобы ничего не приходило и не уходило. Во-вторых, у энергии имеется большое число различных видов, и для каждого есть своя формула. ‹…› Если мы соберем вместе формулы для всех этих вкладов, то энергия не будет меняться, кроме как в тех случаях, когда она уходит наружу или приходит извне.

Важно осознавать, что в рамках сегодняшней физики мы не знаем, что такое энергия. Мы не считаем, что энергия состоит из маленьких капель точно определенного размера. Вовсе нет. Однако у нас имеются формулы для подсчета некоторой численной величины, и, когда мы складываем все результаты, получается «28»  – всегда одно и то же число. Это абстракция, потому что в ней ничего не говорится ни про механизм, ни про причины, стоящие за различными формулами.”

Фейнмановские лекции по физике, т. 1, гл. 4, § 1

В одной из своих передач из цикла «Сквозь кротовую нору» известный американский артист Морган Фриман озвучивает зрителям такой парадокс:
Я могу выйти из дома, дойти до парка, а потом снова вернуться домой в исходную точку пространства. Но со временем такой фокус провернуть не удаётся. Я не могу вернуться в исходную точку времени. В чём причина?

С точки зрения житейской логики и здравого смысла, ответа не существует. Ответ на этот вопрос даёт теория относительности. Нас окружает не 3-мерное пространство, а нас окружает единое 4-мерное пространство-время. Эта теория была многократно проверена наблюдениями.

Для удобства понимания и проведения точных астрофизических расчётов, физики выделили отдельно 3 пространственных измерения X Y Z, которые мы отлично видим и ощущаем, а также одно перпендикулярное им временное измерение T, которое мы не видим, но при этом интуитивно ощущаем.
Важное замечание – это проблема лишь наших органов чувств, но не устройства Вселенной.

И так у нас есть 4 измерения. Геометрическая наглядная интерпретация, пространство Минковского выглядит так:

Из формул специальной теории относительности можно вывести странное следствие. Интервал между любыми пространственными и временными событиями, выраженный в метрах – есть постоянная величина для любых наблюдателей, в любых системах отсчёта: S^2 = c^2*Δt^2 – Δx^2 – Δy^2 – Δz^2. Это уравнение соблюдается всегда и везде. Совпадение? Не думаю. Гораздо логичнее сказать, что пространство относительно, время относительно, но пространство-время в целом – абсолютно.

Если внимательно посмотреть на рисунок и представить его в объёме, оси пространства и времени не похожи друг на друга, есть различие. Ось времени имеет другое направление. Пространственные составляющие вычитаются из временной составляющей.

Самые нелогичные интуитивно непонятные вещи начинают происходить, когда мы попытаемся получить численные значения этих составляющих. Даже когда я сижу на стуле, и нахожусь в состоянии пространственного покоя, я перемещаюсь по временной оси за секунду на расстояние 300000 км (больше 7 экваторов). Получается – покой нам только снится.

Я могу прогуляться в парк, пройти 5 километров за 1 час, но эти 5 километров – это ничтожно малый промежуток по сравнению с моим временным перемещением. Оказывается на самом деле,  я за этот 1 час пролетел в пространстве-времени примерно 300000 * 3600 = 1 млрд. км. То, что я этого не почувствовал, лишь проблема моих органов чувств, но не устройства Вселенной. Да, безусловно я могу повернуть назад, потратить ещё 1 час, снова пройти 5 км и снова оказаться в исходной точке пространства. Но это происходит только потому, что 5 км/ч сквозь пространство – для меня не проблема.

Повышая скорость моего движения, я мог бы увеличить пространственные промежутки, и таким образом сократить время, но для этого необходимо хотя приблизиться к скорости света (при перемещении чисто сквозь пространство). А для того чтобы вернуться в исходную точку, время должно пойти в отрицательном направлении. Для этого необходимо превысить скорость света в пространстве.

Ну а поскольку для тел, имеющих массу покоя, перемещаться сквозь пространство со скоростью света невозможно, и уж тем более превысить её, то эта единственная лазейка для возвращения в исходную точку времени тоже оказывается закрыта. Остаётся только признать, что время во Вселенной точно есть, остановить и обогнать его известными способами не получается. Может быть варп поможет в этом вопросе, но это фантастика.

Не скажу, что до конца разобрался, но некоторую логику, спасибо Владимиру Бомбину, надыбал. Однако, основное, пока разбирался столько красивых фото увидел, что грех частью не поделиться.
Северные сияния вещь простая. Солнце выплюнуло частицы (солнечный ветер), они долетели до Земли, возбудили атомы в атмосфере, атомы рекомбинировали и мы получили возможность наблюдать их спектр во всей красе на небе. Пока любопытна здесь величина скорости частиц (долетают до нас (150 млн км) за 2-3 дня, т. е. 500-800 км/сек) + то, что солнечный ветер накрывает всю Землю, даже если у него расходимость как у луча лазера (10тыс км/150 млн км ~ 10^-4).
Северное сияние бывает везде, где есть север. Его видели даже на Юпитере.

(слева Земля со спутника; справа Юпитер).
Север/юг нужен, т. к. заряженные частицы дрейфуют к магнитному полюсу по линиям магнитного поля.

(справа невозмущённое поле; слева возмущённые солнечным ветром радиационные пояса, «авроральный» это про северные сияния)
Теперь о цвете/спектре. На Юпитере возбуждается /рекомбинирует водород и снимок сделан в ультрафиолете.
На Земле мы наблюдаем глазом спектр азота и кислорода. Выглядят они так:

красный, жёлто-оранжевый, зелёный, синий. Поэтому «нормальный» вид сияния — многоцветный, как на правой фотграфии (Омск).

Меня удивила левая (южная) фотография (все фото от 5 ноября). Откуда такая монохроматичность? Объяснение из ФИАНа  Вячеслава Авдеева– «Его цвет зависит от высоты, с которой идёт излучение. При большей плотности газов, то есть в более низких слоях атмосферы, оно бывает зелёным, а в верхних слоях – красным.», меня не устроило. Спектр от плотности не зависит, а распределение газов по высоте:

Кислорода везде больше азота. Только в слое F₂ – 9:1 ; F₁ -2:1 . Почему чем меньше кислорода, тем лучше видны его линии и именно зелёные непонятно.
Однако, известен ответ на древний вопрос: «Почему Солнце красно на закате?» А потому, что длинноволновое излучение слабее рассеивается (потому и «стоп» на светофоре — красный). Издали, а на юге как солнечный ветер ни бушуй, но северное сияние ближе к полюсу, нежели к Крыму, красный виден лучше. Зелёный и синий просто не дошли. Именно здесь основная причина красного северного сияния в Крыму.

Машина времени есть у каждого из нас: то, что переносит в прошлое — воспоминания; то, что уносит в будущее — мечты.